
第2話 境界値分析とは
みなさん、こんにちは。鎌倉です。第1話では、テストを行う際の入力値を選定する技法として「同値分割法」をご紹介しました。第2話でも、入力値を選定する技法をご紹介したいと思います。今回のテーマは「境界値分析」です。
境界値分析のしくみ
境界値分析は、前回取り上げた同値分割法と同様にブラックボックステストの技法のひとつです。一定範囲に含まれる入力値が全て同じ挙動となる場合、範囲にギリギリ入る値とギリギリ入らない値をピックアップでテストし、境界線付近の挙動に誤りがないかを確認します。
境界値分析の考え方
境界値分析でも同値分割法と同様に入力値を同値クラスに分けて考えますが、同値分割法と大きく違うのは、同値クラスの条件を不等式で表現できる場合のみ利用可能な点です。
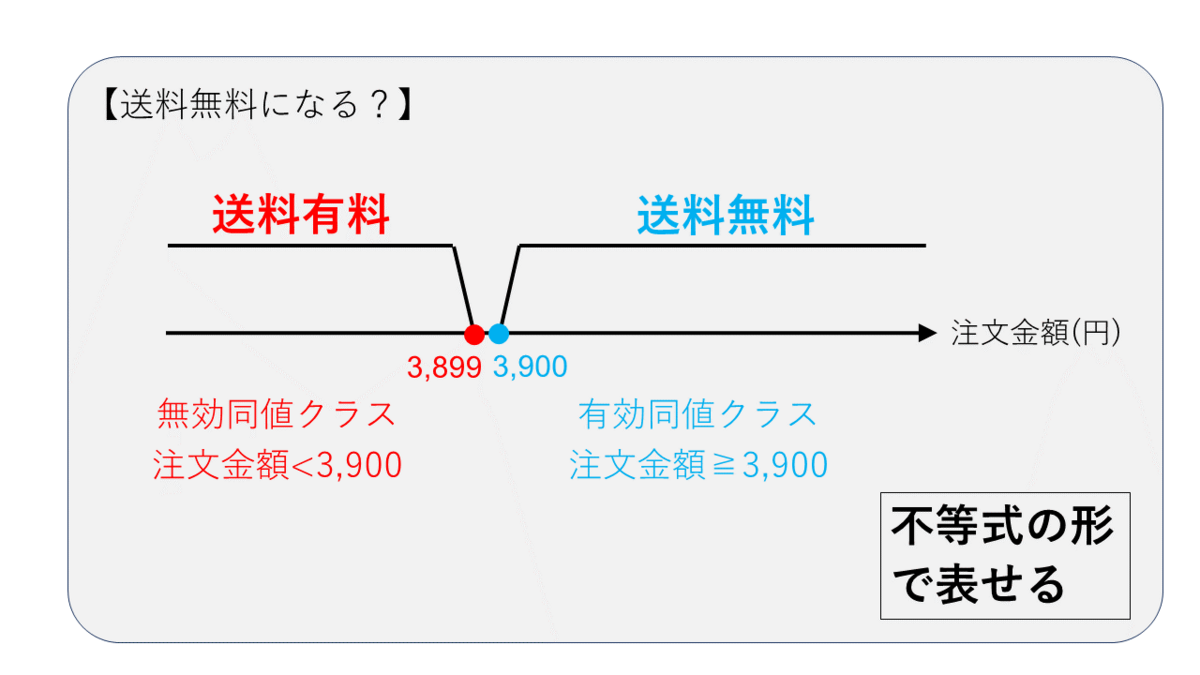
たとえば「注文金額が3,900円以上の場合、送料を無料にする」という判定処理であれば、有効同値クラスを不等式で表現できるため境界値分析を利用可能です。
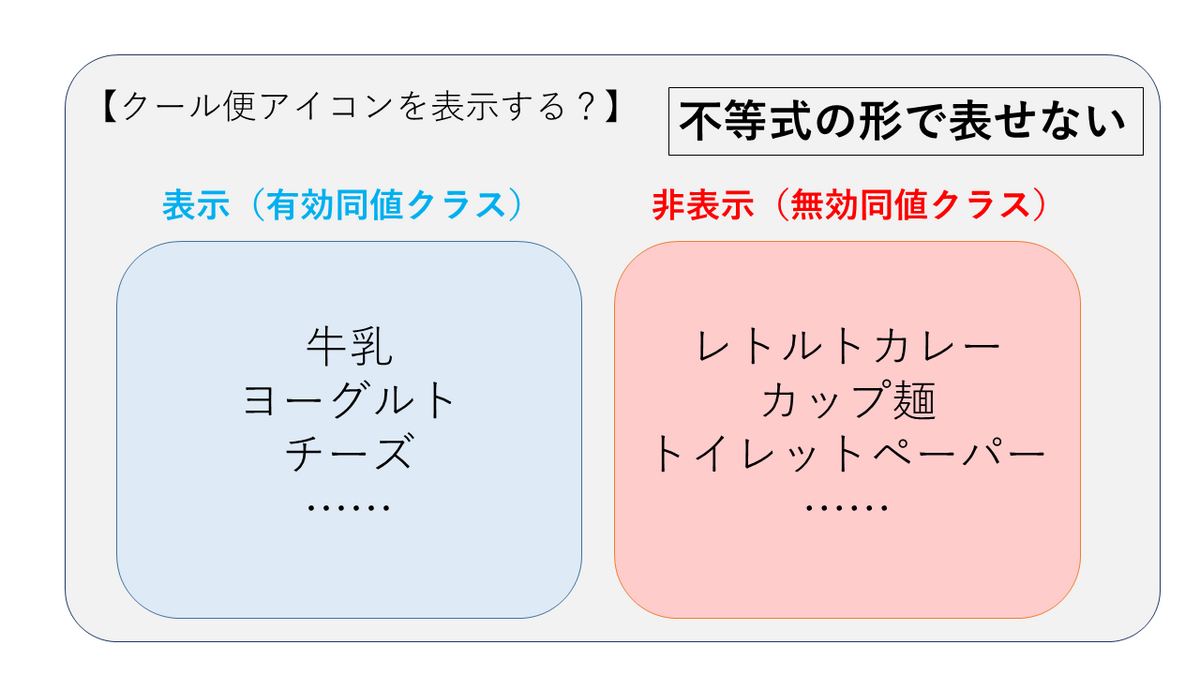
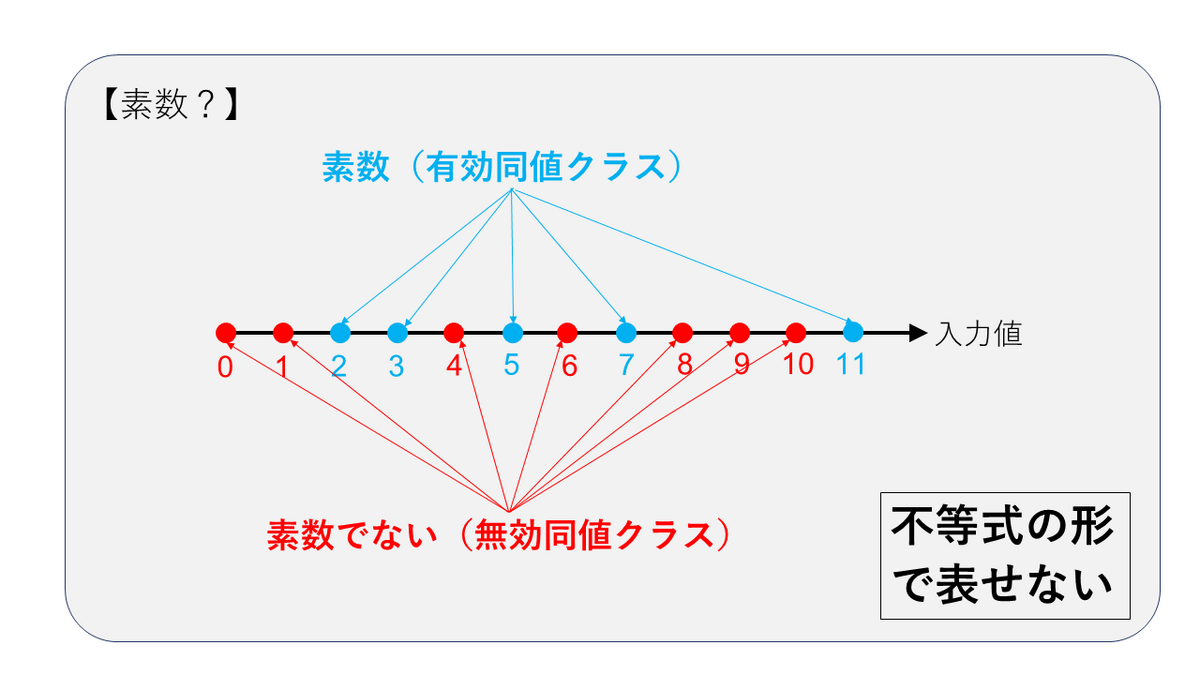
「商品の要冷蔵フラグがONの場合、クール便アイコンを表示する」とか「入力された整数が素数ならば太字で表示する」といった判定処理では、同値クラスの条件が不等式では表現できないため、境界値分析は利用できません。
境界値の見つけ方
「注文金額が3,900円以上の場合、送料を無料にする」の例で境界値の見つけ方を説明します。
有効同値クラス:注文金額≧3,900円
無効同値クラス:注文金額<3,900円
のように不等式の形で表現できますので、境界値分析が利用可能です。
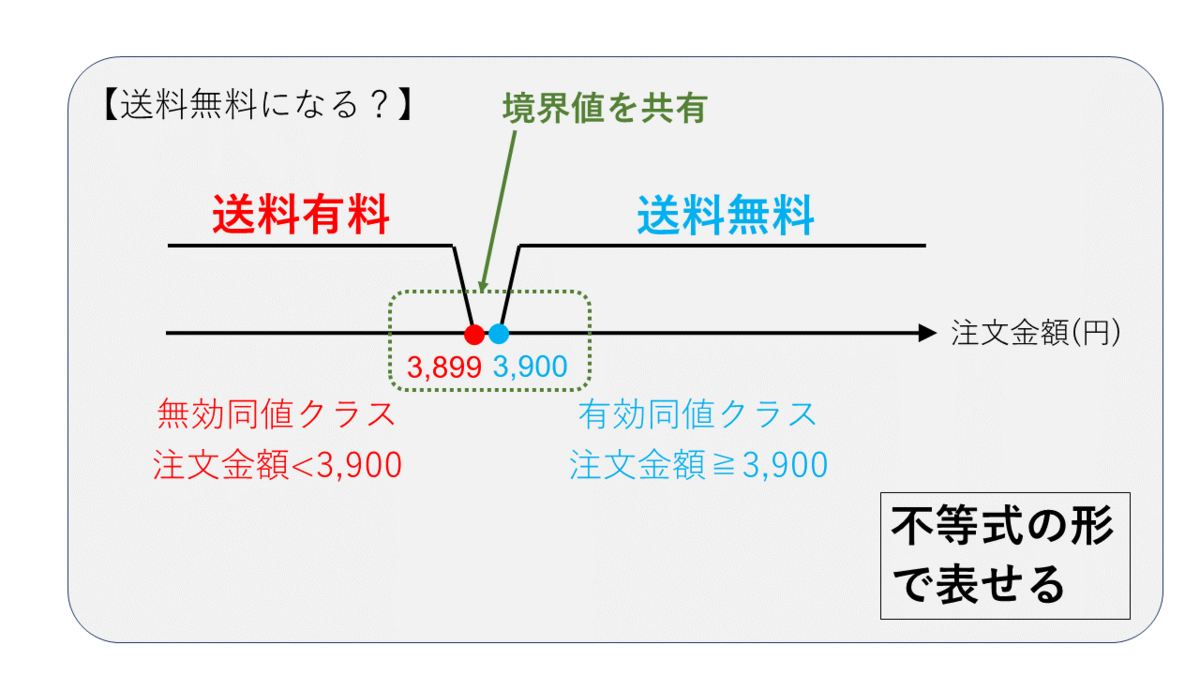
まずは有効同値クラスに着目してみましょう。有効同値クラスの範囲にギリギリ入る値は3,900、ギリギリ入らない値は3,899ですね。したがって、この2つの値は境界値としてテストする必要があります。
次に無効同値クラスに着目すると、範囲にギリギリ入る値は3,899、ギリギリ入らない値は3,900となるので、有効同値クラスで選んだ境界値と一致します。
このように、数直線上で隣接している同値クラスは境界値を共有します。同じ値を2回テストしないように注意してください。
境界値分析には同値クラスの範囲にギリギリ入る値とギリギリ入らない値の2つをテストする「2値の境界値分析」と、境界線の値と隣接する両隣の値の計3箇所をテストする「3値の境界値分析」があります。
本稿は初心者向けの構成のため、ぐるなび社内のテストでもよく利用されており、考え方が簡単な「2値の境界値分析」に絞って説明しています。
テストケースを設計してみよう
それでは、今回も例題をもとにテストケース(テスト項目)を設計してみましょう。
【例題】
あるECサイトで注文金額に応じて送料の割引を判定する処理のテストを設計しています。仕様は次の通りです。
【送料割引の仕様】
①注文金額の1円未満は切捨て
②注文金額が3,900円以上の場合、「送料無料」を表示する
③注文金額が2,000円以上3,900円未満の場合、「送料半額」を表示する
④注文金額が0円以上2,000円未満の場合、「割引なし」を表示する
⑤注文金額はマイナスにならないものとする
この機能を境界値分析でテストする場合、必要なテストケースはいくつでしょうか。
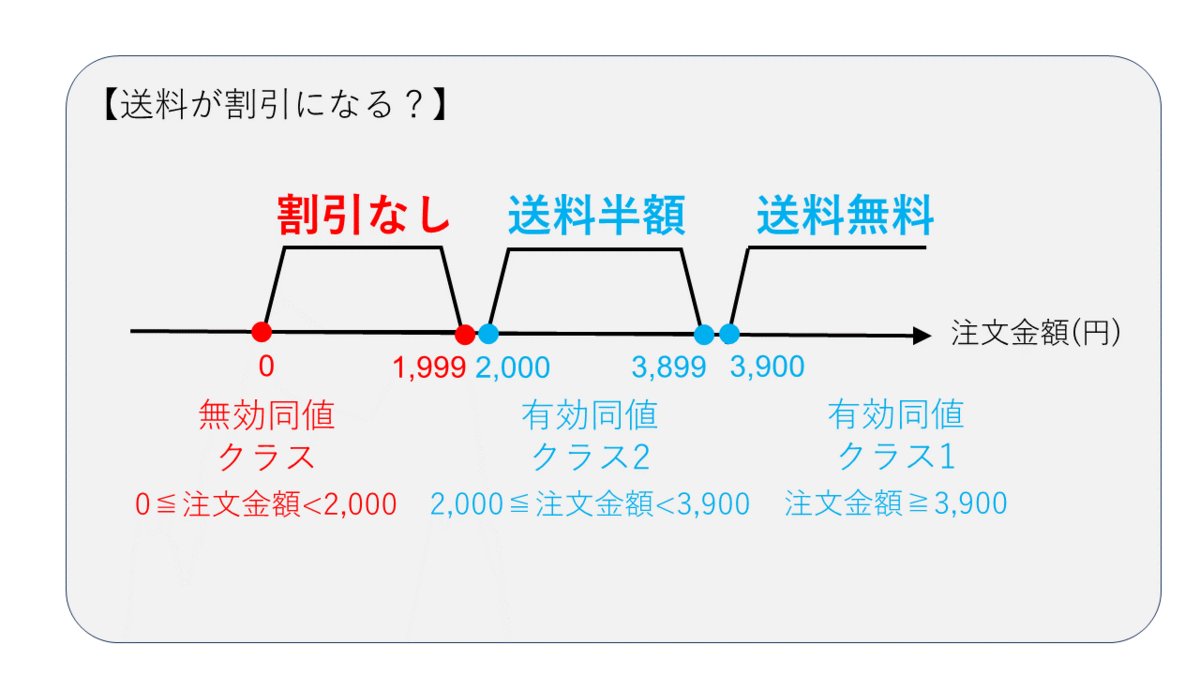
同値クラスに分割
まずは有効同値クラスと無効同値クラスに分割しましょう。この例題では送料が割引になる有効同値クラスが2つ、送料が割引にならない無効同値クラスが1つ存在します。 各同値クラスの条件は、
有効同値クラス1(送料無料):注文金額≧3,900円
有効同値クラス2(送料半額):2,000円≦注文金額<3,900円
無効同値クラス(割引対象外):0円≦注文金額<2,000円
のように不等式を使って表現することができます。
境界値の特定
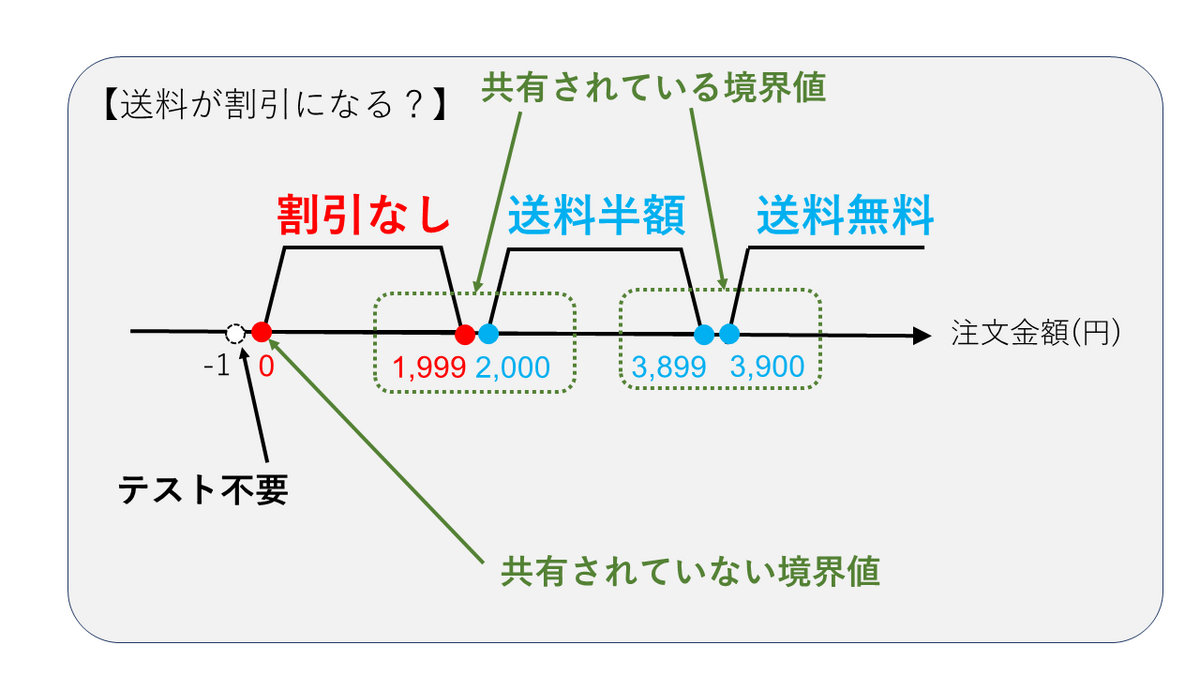
次は分割された同値クラスをもとに、境界値を特定しましょう。 有効同値クラス1にギリギリ入る値は3,900、ギリギリ入らない値は3,899です。この2つの値は境界値としてテストする必要があります。
有効同値クラス2にギリギリ入る値は3,899と2,000、ギリギリ入らない値は3,900と1,999です。3,899と3,900は有効同値クラス1と境界値を共有していますね。重複をさけるため、2,000と1,999の2つだけをテストする境界値に追加する必要があります。
無効同値クラスにギリギリ入る値は1,999と0、ギリギリ入らない値は2,000と-1です。仕様の⑤に「注文金額はマイナスにならないものとする」とありますので、-1はテスト対象から除外しましょう。 1,999と2,000は有効同値クラス2と境界値を共有しているので、重複しないように0だけをテストする境界値に追加すればOKです。
以上の結果をまとめると、テストする必要がある境界値は0、1,999、2,000、3,899、3,900の5つであることがわかりました。
テストケースに落とし込む
それでは、特定できた境界値をもとにテストケースを作成しましょう。 実際のテストケースより少し簡略化していますが、次のようなイメージです。

このように、5パターンをテストすればよいことになります。
実践演習
最後は実践演習です。次の問題にチャレンジしてみましょう。
【問題】
ある情報サイトにおいて、年齢を入力すると国民年金の加入対象年齢かどうか判定する機能を実装しています。 年齢の入力は画面内のプルダウンリストで行い、利用者が0から150までの整数を選択する仕様で、改ざんによる不正な値の考慮は不要です。 入力された年齢に応じて、次のいずれかのメッセージを表示します。
【表示メッセージの仕様】
① 20歳以上60歳未満の場合は「加入対象」を表示
② 20歳未満または60歳以上の場合は「加入対象外」を表示
この機能を境界値分析でテストする場合、必要なテストケースはいくつでしょうか。
正解と解説
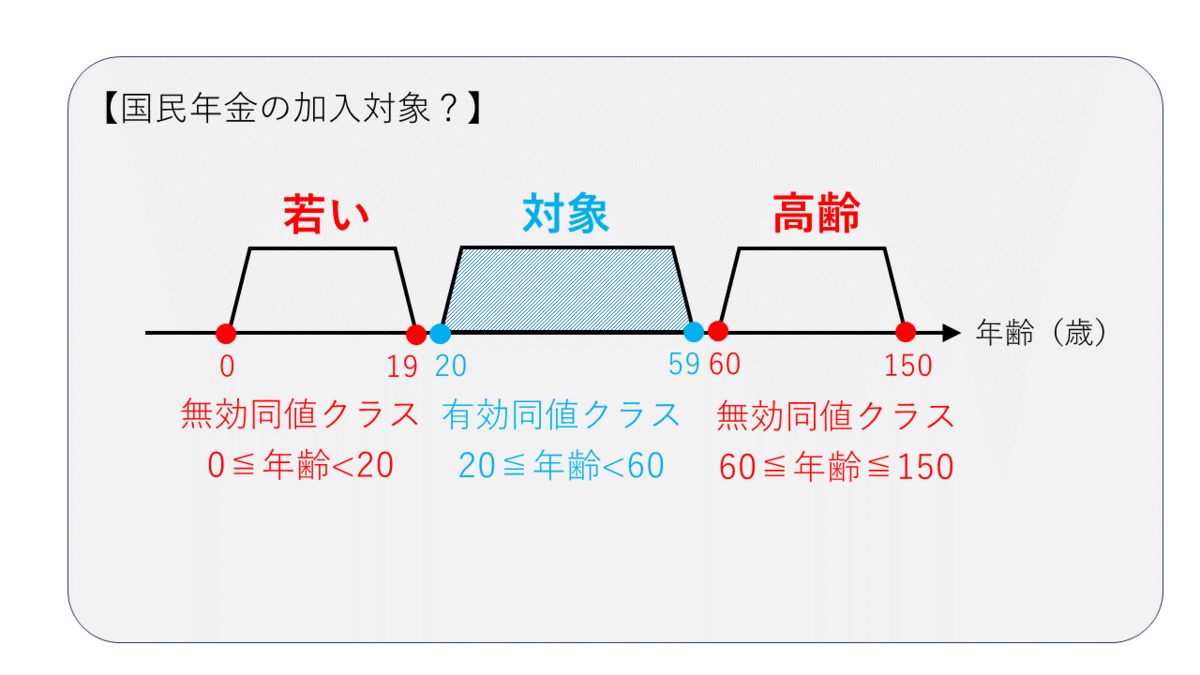
まずは有効同値クラスと無効同値クラスに分割しましょう。例題では国民年金の加入対象年齢かどうかを判定していますので、加入対象の年齢が有効同値クラスです。 20歳≦年齢<60歳のように不等式で表せるので、境界値分析を用いることができますね。
無効同値クラスは、0歳≦年齢<20歳(若いので加入対象ではない)、60歳≦年齢≦150歳(高齢なので加入対象ではない)の2つがあります。
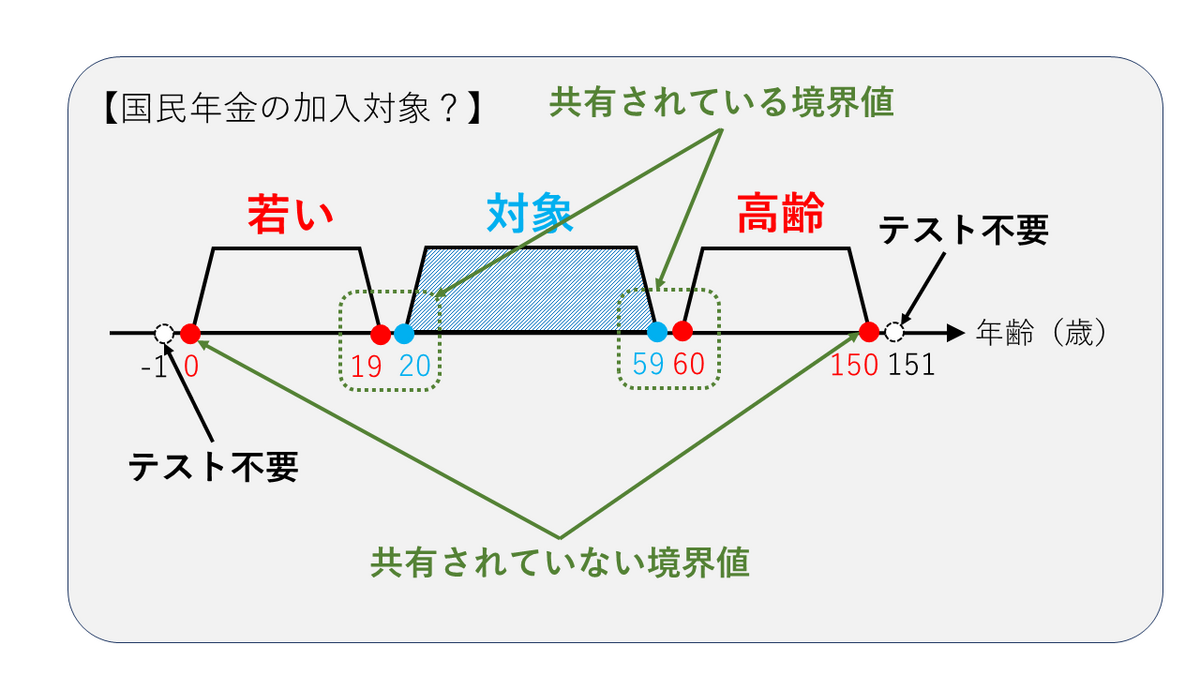
次は分割された同値クラスをもとに、境界値を特定しましょう。 有効同値クラスにギリギリ入る値は20歳と59歳です。ギリギリ入らない値は19歳と60歳となります。これらの境界値は隣接する無効クラスと境界値を共有していますね。
この他に、無効同値クラスにギリギリ入っている両端の0歳と150歳も境界値としてテストする必要があります。 無効同値クラスにギリギリ入らない-1歳と151歳については、問題文に「利用者が0から150までの整数を選択する仕様で、改ざんによる不正な値の考慮は不要」とありますので、境界値に含める必要はありません。
もしもユーザーがキーボードから入力するシステムで、不正な値も入力される可能性がある場合には境界値に含める必要があります。
最後に、特定できた境界値をもとにテストケースを作成しましょう。 入力された年齢が0、19、 20、59、60、150のケースをテストする必要があります。 実際のテストケースより少し簡略化していますが、次のようなイメージです。

上の表のとおり、6つのテストケースが必要なことがわかりました。
まとめ
今回はブラックボックステストのテスト技法、「境界値分析」をご紹介しました。押さえておくべきポイントとしては、
- 同値分割法と同様に入力値を「同値クラス」に分割する
- 同値クラスの条件を不等式の形で表現できる場合に利用可能
- 各同値クラスの範囲に「ギリギリ入る値」と「ギリギリ入らない値」を「境界値」としてテストする
- 隣接する同値クラスは境界値を共有するため、テストすべき値を列挙するときは重複に注意する
といったものがあります。境界値分析を使うと同値クラスの境目だけ確認すればよいので、効率よくテストが進められそうですね。
第3話では、同値分割法と境界値分析を組み合わせて使う方法をご紹介します。どうぞお楽しみに!
